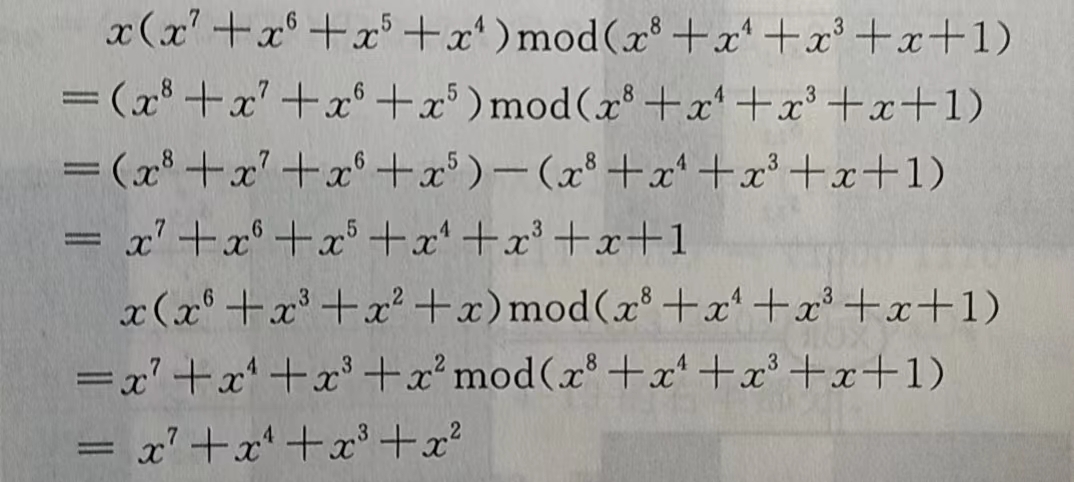密码学之AES算法
一、AES 算法介绍
AES 的全称是 Advanced Encryption Standard,意思是高级加密标准。它的出现主要是为了取代 DES 加密算法的,因为我们都知道 DES 算法的密钥长度是 56Bit,因此算法的理论安全强度是 2 的 56 次方。但二十世纪中后期正是计算机飞速发展的阶段,元器件制造工艺的进步使得计算机的处理能力越来越强,虽然出现了 3DES 的加密方法,但由于它的加密时间是 DES 算法的 3 倍多,64Bit 的分组大小相对较小,所以还是不能满足人们对安全性的要求。于是 1997 年 1 月 2 号,美国国家标准技术研究所宣布希望征集高级加密标准,用以取代 DES。AES 也得到了全世界很多密码工作者的响应,先后有很多人提交了自己设计的算法。最终有 5 个候选算法进入最后一轮:Rijndael,Serpent,Twofish,RC6 和 MARS。最终经过安全性分析、软硬件性能评估等严格的步骤,Rijndael 算法获胜。
在密码标准征集中,所有 AES 候选提交方案都必须满足以下标准:
- 分组大小为 128 位的分组密码。
- 必须支持三种密码标准:128 位、192 位和 256 位。
- 比提交的其他算法更安全。
- 在软件和硬件实现上都很高效。
AES 密码与分组密码 Rijndael 基本上完全一致,Rijndael 分组大小和密钥大小都可以为 128 位、192 位和 256 位。然而 AES 只要求分组大小为 128 位,因此只有分组长度为 128Bit 的 Rijndael 才称为 AES 算法。本文只对分组大小 128 位,密钥长度也为 128 位的 Rijndael 算法进行分析。密钥长度为 192 位和 256 位的处理方式和 128 位的处理方式类似,只不过密钥长度每增加 64 位,算法的循环次数就增加 2 轮,128 位循环 10 轮、192 位循环 12 轮、256 位循环 14 轮。
二、原理
1.流程
AES 算法(即 Rijndael 算法)是一个对称分组密码算法。数据分组长度必须是 128 bits,使用的密钥长度为 128,192 或 256 bits。对于三种不同密钥长度的 AES 算法,分别称为“AES-128”、“AES-192”、“AES-256”。(Rijndael 的设计还可以处理其它的分组长度和密钥长度,但 AES 标准中没有采用)
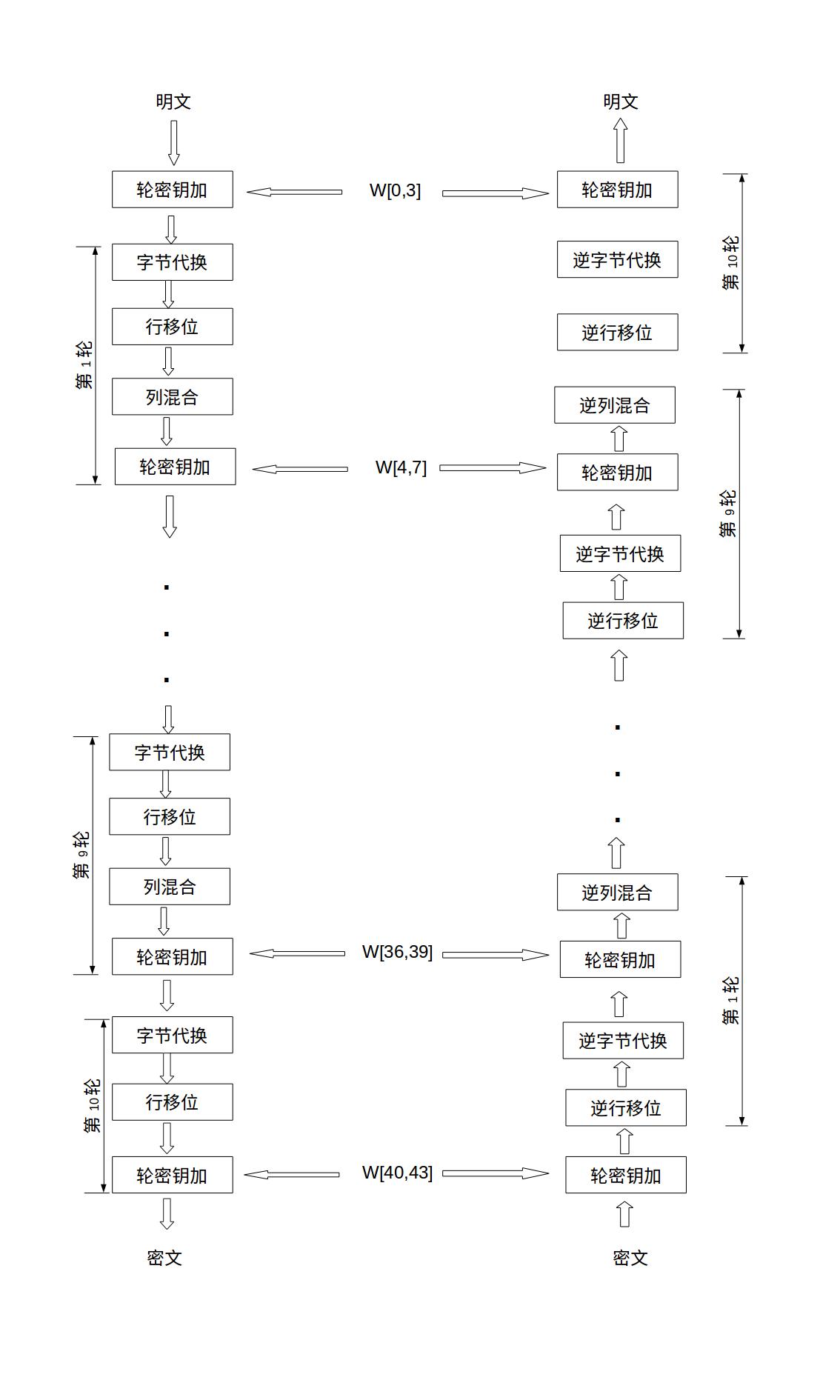
下图是 AES 加密解密的整体流程图:
2.注意
-
这里用的是
AES-128,因此密钥长度128,AES迭代次数10轮 -
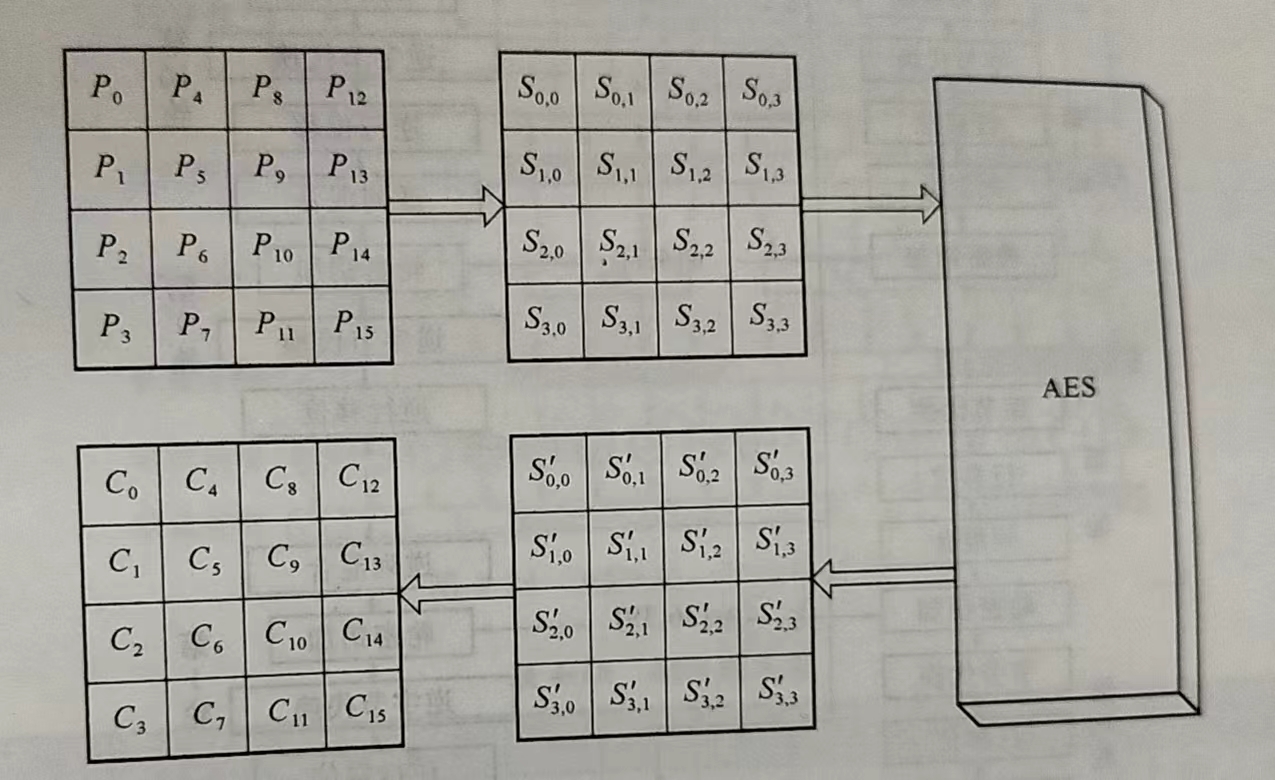
AES 的处理单位是字节,128 位的输入明文分组 P 和输入密钥 K 都被分成 16 个字节,一般地,明文分组用以字节为单位的正方形矩阵描述,称为状态(State)矩阵
注意矩阵中字节的排序顺序是从上到下,从左到右
-
这里我们需要知道 3 个符号:
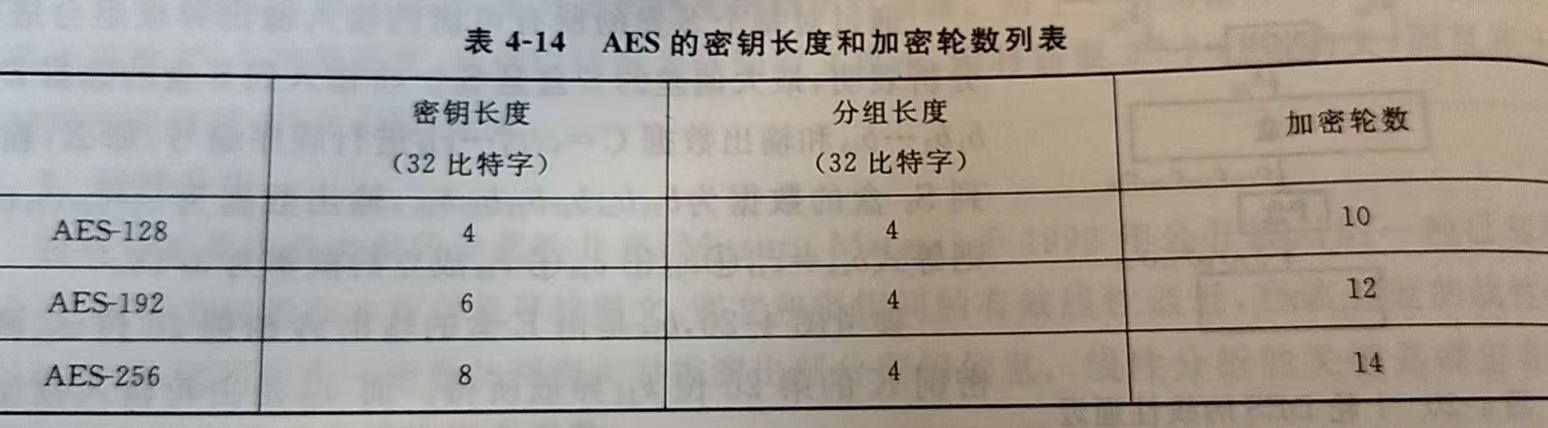
Nb—— 状态 State 包含的列(32-bit 字)的个数,也就是说Nb=4;Nk—— 密钥包含的 32-bit 字的个数,也就是说Nk=4,6 或 8;Nr—— 加密的轮数,对于不同密钥长度,轮数不一样,具体如下图所示:
注意只有
Nr - 1次是相同的,最后一轮都少了列混合
下面分为密钥扩展、分组加密、分组解密三个部分来讲 AES 算法,C++代码在后面
三、AES 算法
1.密钥扩展
1.1 流程
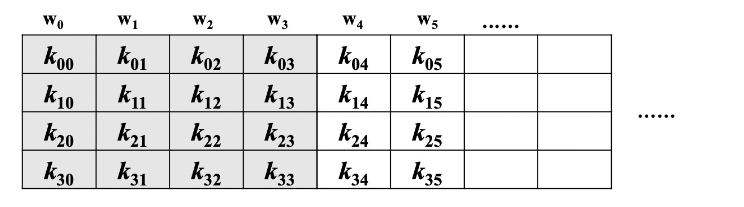
AES 算法通过密钥扩展程序(Key Expansion)将用户输入的密钥 K 扩展生成 Nb(Nr+1)个字,存放在一个线性数组w[Nb*(Nr+1)]中。具体如下:
-
位置变换函数
RotWord(),接受一个字[a0, a1, a2, a3]作为输入,循环左移一个字节后输出[a1, a2, a3, a0]。 -
S盒变换函数SubWord(),接受一个字[a0, a1, a2, a3]作为输入。S盒是一个 16x16 的表,其中每一个元素是一个字节。对于输入的每一个字节,前四位组成十六进制数x作为行号,后四位组成的十六进制数y作为列号,查找表中对应的值。最后函数输出4个新字节组成的 32-bit 字。 -
轮常数
Rcon[],如何计算的就不说了,直接把它当做常量数组。 -
扩展密钥数组
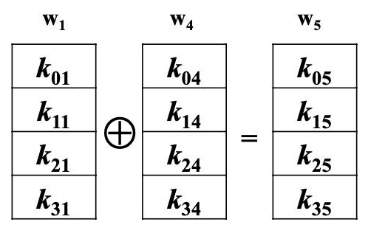
w[]的前Nk个元素就是外部密钥K,以后的元素w[i]等于它前一个元素w[i-1]与前第Nk个元素w[i-Nk]的异或,即w[i] = w[i-1] XOR w[i-Nk];但若i为Nk的倍数,则w[i] = w[i-Nk] XOR SubWord(RotWord(w[i-1])) XOR Rcon[i/Nk-1]。
1.2 伪代码
1.2.1 $ N_k <= 6$(主)
即适合 AES-128 和 AES-192,这里只以 AES-128 为例子
1 |
|
1.2.2 $ N_k > 6$(略)
即适合 AES-256,本篇文章不予实现,但给出伪代码
1 | KeyExpansion(byte Key[4 * Nk], W[Nb * (Nr + 1)]) { |
1.2.3 $ N_k $大小的区别区别
当$ i - 4 $为$ N_k $的整数倍时,须先将前一个子$ W[i - 1]$经过 SubByte变换(S 盒变换)
1.3 代码实现
1.3.1 代码
1 |
|
1.3.2 结果
1 | KEY IS: 2b 7e 15 16 28 ae d2 a6 ab f7 15 88 9 cf 4f 3c |
2.分组加密
2.1 伪代码
1 | Cipher(byte in[4*Nb], byte out[4*Nb], word w[Nb*Nr+1]) |
从伪代码描述中可以看出,AES 加密时涉及到的子程序有SubBytes()、ShiftRows()、MixColumns()和AddRoundKey(),即字节替换,位位移,列混合,密钥轮加。不清楚请自动移步到右侧二、原理的流程图中
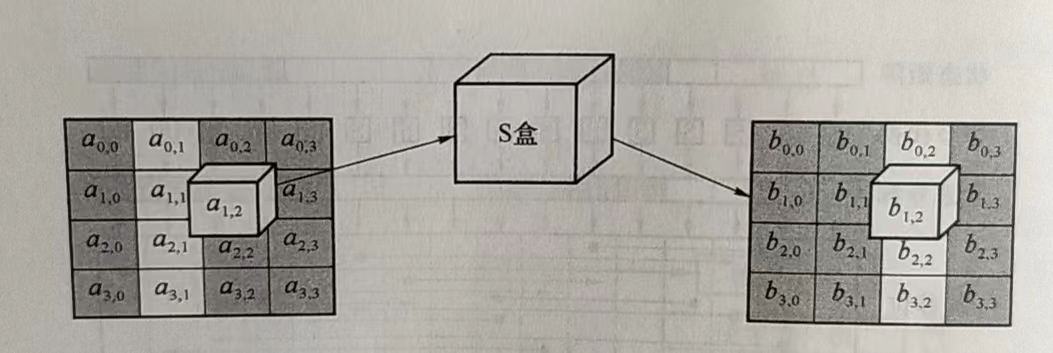
2.2 字节替换-SubBytes()
在密钥扩展部分已经讲过了,S盒是一个 16 行 16 列的表,表中每个元素都是一个字节。S盒变换很简单:函数SubBytes()接受一个 4x4 的字节矩阵作为输入,对其中的每个字节,前四位组成十六进制数x作为行号,后四位组成的十六进制数 y 作为列号,查找表中对应的值替换原来位置上的字节。
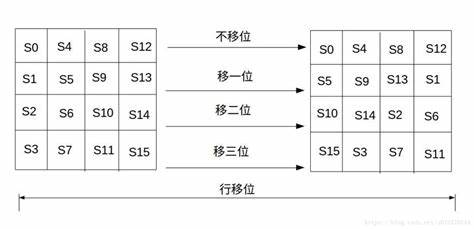
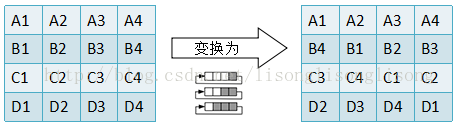
2.3 行位移-ShiftRows()
AES 的行移位也是一个简单的左循环移位操作。当密钥长度为128比特时,状态矩阵的第0行左移0字节,第1行左移1字节,第2行左移2字节,第3行左移3字节
2.4 列混合-MixColumns()
列混合变换是通过矩阵相乘来实现的,经行移位后的状态矩阵与固定的矩阵(即下图左乘后面的矩阵)相乘,得到混淆后的状态矩阵。
这里需要注意的是矩阵元素中的乘法和加法都是定义在居于$Z_2[x]$中不可约多项式$ m(x) = x^8 + x^4 + x^3 + x + 1 $ 构造的$ GF(2^8) $ 上的二元运算。加法等价于两个字节的异或,乘法运算比较复杂,是伽罗华域(GF,有限域)上的乘法
请仔细阅读下面例子,获取计算·2和·3
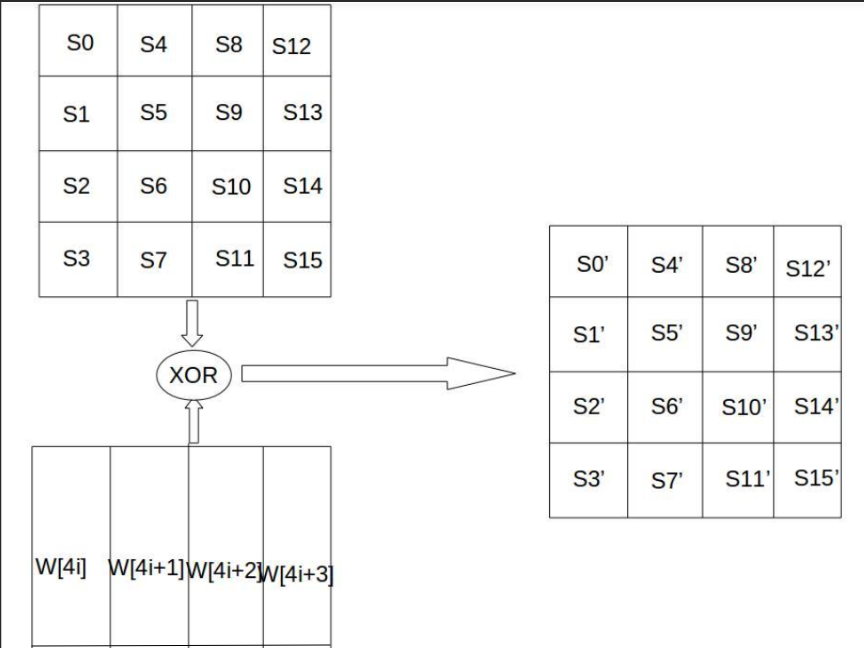
2.5 轮密钥加-AddRoundKey()
扩展密钥只参与了这一步。根据当前加密的轮数,用w[]中的4个扩展密钥与矩阵的 4 个列进行按位异或,即将128位轮密钥Ki同状态矩阵中的数据进行逐位异或操作。
3. 分组解密
3.1 伪代码
1 | InvCipher(byte in[4*Nb], byte out[4*Nb], word w[Nb*Nr+1]) |
从伪代码描述中可以看出,AES 加密时涉及到的子程序有SubBytes()、ShiftRows()、MixColumns()和AddRoundKey()。下面我们一个一个进行介绍:
3.2 逆行变换-InvShiftRows()
上面讲到ShiftRows()是对矩阵的每一行进行循环左移,所以InvShiftRows()是对矩阵每一行进行循环右移。
3.3 逆 S 盒变换-InvSubBytes()
与 S 盒变换一样,也是查表,查表的方式也一样,只不过查的是另外一个置换表(S-Box 的逆表,下面 C++代码中有)。
3.4 逆列变换-InvMixColumns()
与列变换的方式一样,只不过计算公式的系数矩阵发生了变化。详细知识请自行去了解,这里我们只需要记住总结的函数即可,如下图:
四、C++代码
1. 代码
有些函数的注释我咋上面密钥扩展中已经写过了,还有解密的过程和加密十分相似,看懂加密解密自然不在话下,这些竹丝便不再重复,若有其他问题请评论提问( ̄︶ ̄)↗
先看懂上面一步一步来 ╰(‵□′)╯
1 | //超详细注释来袭 ψ(`∇´)ψ |
2. 注意
有限域$ GF(2^8) $上的乘法改用查表的方式实现,AES的加密速度马上提升 80% 以上,所以建议最好使用查表的方式。下面是 AES 算法中用到的 6个乘法结果表:
1 | byte Mul_02[256] = { |
五、总结
AES 的优势
-
更高的安全性:
AES提供了更高的安全性,因为它支持更长的密钥长度(128 比特、192 比特和 256 比特),这使得密码破解更加困难。相比之下,DES 使用 56 位密钥,相对容易受到暴力破解攻击。 -
更快的加密速度:
AES的算法结构允许更高效的硬件和软件实现,因此它通常比DES更快。这是由于其更简单的替代和置换结构,以及较长的密钥长度。 -
更好的密码学设计:
AES的设计经过了广泛的密码学研究和审查,以确保其强大的安全性。相比之下,DES 已经过时,已经受到多种攻击的影响,包括差分攻击和线性攻击。 -
支持多种密钥长度:
AES允许选择不同长度的密钥,以适应不同安全需求。这样,可以根据具体应用选择 128 位、192 位或 256 位密钥长度。 -
广泛采用:
AES已经被广泛采用,被许多组织和国家用作数据加密的标准,包括美国政府。
AES 的缺点
-
高硬件成本: 虽然
AES的算法结构更高效,但实现硬件版本仍然可能比DES更昂贵。这可能会对资源有限的嵌入式系统造成一定负担。 -
不支持较长的块长度:
AES只支持128位的块长度,而某些应用需要更长的块长度。这可能需要进行分组加密,增加了复杂性。
总的来说,AES 是一安全、高效且现代的对称加密算法,相对于 DES 具有更多的优势。虽然它可能不是完美的,但它是当前广泛应用的加密标准之一,可满足多种安全需求。